Vinyl, CD, and That Annoying Friend you wanna silence...

I want to tell you a funny situation, that happens to me at least twice a year, when I go back in Italy for my holidays. I use to go there to meet old friends, take care of boring bureaucracy, have great beers and food. But it's not always that blessing - everybody has that friend. He's usually an elitist of something - it may be football, technology, food and drink, tourism (yes, I know someone who's such a PitA!), and so on. 

One of the most dreadful and dangerous is the music-elitist. Not only does he erode your patience with his theories about this and that band - he goes far beyond. He wants to teach you "HOW" you must listen to music, and quite often he's also willing to pontificate his views on technology unto you. So, between a "Ghost are not metal" and a "Lady Gaga is poor man's Madonna", he starts giving you some unneeded lessons. The most frequent one is when he starts pointing out the infinite supremacy of vinyls over CDs. Later on I will tell you the best argument to shut his mouth off and make him look like a moron, but first: is he right about vinyl? We want to serve this Mr. Know-it-all a slice of humble pie, without giving him the chance to do the same to us..

So, why do people say that CDs are somehow worse than Vinyl? Is that true?

The answer is... MEH. 

First, let's understand how vinyl works. Vinyl is an analog format that stores sound information physically. When you look at a vinyl record, you can see thin grooves that run across its surface. These grooves are actually a physical representation of the sound wave.

When the turntable's needle is placed on the vinyl, it moves along the grooves, which are cut in a spiral pattern on the record. The physical variations in the grooves (their depth and width) correspond to the original sound waves. The needle, connected to a transducer, vibrates according to the irregularities of the groove. These vibrations are then converted into electrical signals, which the turntable sends to the amplifier, and are finally transformed into sound through the speakers.

Conversely, CD store data in digital format, as a long series of bits (i.e., instances of two different values, typically 0 and 1). The surface of the disc is made of transparent plastic and has a reflective metal coating, usually aluminum, on which microscopic depressions called "pits" and "lands" are engraved. The "pits" represent the transitions from 1 to 0 (and vice versa), while the "lands" represent the absence of transitions, meaning continuity in the bits. 

When a CD is inserted into the player, a laser reads these depressions as the disc spins. The laser reflects off the surface of the disc, and the presence or absence of reflection, depending on the "pits" and "lands," is interpreted as a sequence of 1s and 0s. These bits are then converted into electrical signals and decoded to reproduce the original sound.

We have introduced two concepts, analogic and digital sound. 

Basically, an analog variable can take all values between two given numbers. In theory, you can represent a constant such as π, or 1/7, with the highest possible precision. On the other hand, a digital variable can only hold two states—presence and absence of signals. One might think that this system can only represent integer numbers. This is not true, actually; it is possible to represent real numbers with a pretty good approximation. There is a post on my other blog where you can see how numbers are represented in a computer. However, the key takeaway here is that not all real numbers can be properly represented with bits (and bytes!). In technical terms, a new set of numbers is defined, usually called "Machine numbers." This is a subset of real numbers containing only the numbers that can be represented in a given computer architecture. For the sake of this discussion, assume that there is a standard architecture for digital music (and yes, there is one, if you're wondering. It is called CD-DA or Red Book, developed by Sony and Philips in 1980).

So - there are two types of variables: analog and digital. Analog variables are perfect to represent CONTINUOUS variables, whereas Digital variables work well with DISCRETE variables. What is the difference? Let's not get into the technical details of epsilon-delta definitions for the continuity - just see it like this: a continuous function is one whose graph can be drawn without lifting the pen from the sheet. A better example: when you open a faucet, this can theoretically deliver any quantity of water between null and the greatest quantity of litres per second it can deliver. On the other hand, a traditional switch has only two positions - on or off. This is a discrete variable - there is no possibility to represent ALL values between two numbers (well, the discussion here is quite complex, for there are rational numbers - i. e., fractions). From this perspective, one may think that discrete variables are less precise than continuous ones. However this would be an over-simplification - we'll get to this.

According to the Red book: 

• Sampling frequency is 44.1 kHz. 
• Sampling depth is 16 bit. 

What does it mean? We need to introduce the concept of sampling.

Sampling rate (or frequency) is nothing more than the number of measurements per seconds. This magnitude is measured in Hertz, or times per second. Therefore if a sound is sampled at 44.1 kHZ, in one second there have been more than 44100 measurements. To give you a sense of scale: if you counted aloud from 1 to 44100, it'd take you something between six hours and six hours and a half. The period of time between two subsequent measurements is called sampling period. 

To go further, we need to make an abstraction: we know that time is a continuous quantity, although we perceive it as a discrete one (we say "it's 5:23" and not "it's 5:23:45.6789...". We accept some approximation). Let's apply this model to time in the sampling context—for us, time is going to be a DISCRETE VALUE (my Physics teacher must be turning in his grave).

We will use the Greek letter $\sigma$ to denote the value of the sound wave at any given time $t_n$, so the full notation will be $\sigma(t_n)$. On the other hand, we will call $T_c$ the sampling period, which is the inverse of the sampling frequency. Therefore, it's easy to see that at a given time $t_n$, the relation $\sigma(t_n) = s(nT_c)$ holds, where $s(t)$ is the value of the continuous waveform, sampled at integer times $t = n$.

We will use the writing $[x_1, x_2, x_3,\dots,x_n]$ to denote an ordered sequence of values.

Consider that in the next images, the frequency is "only" 100 Hz. 100 Hz are roughly 0.22% of 44.100 kHz...

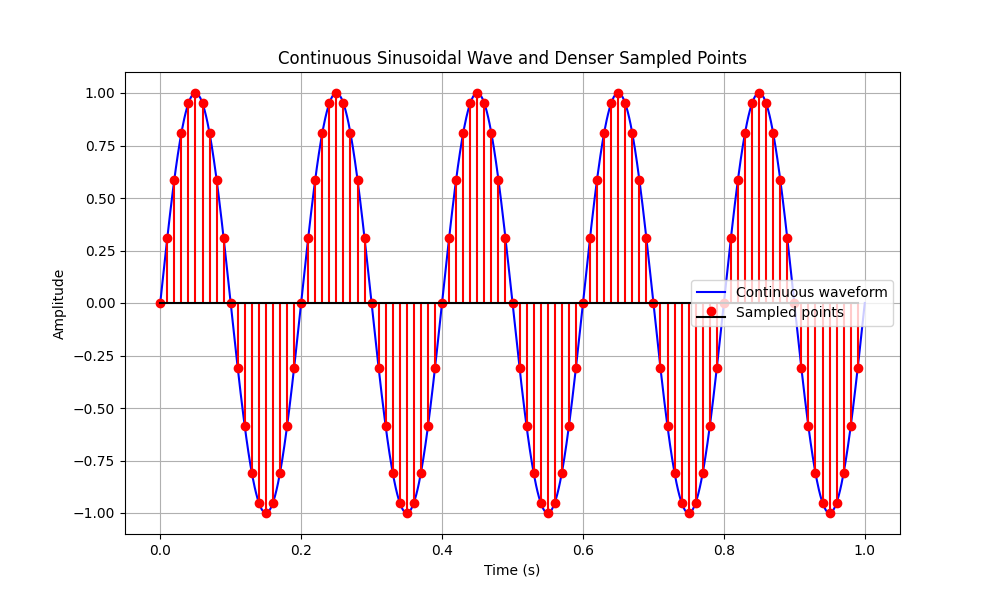
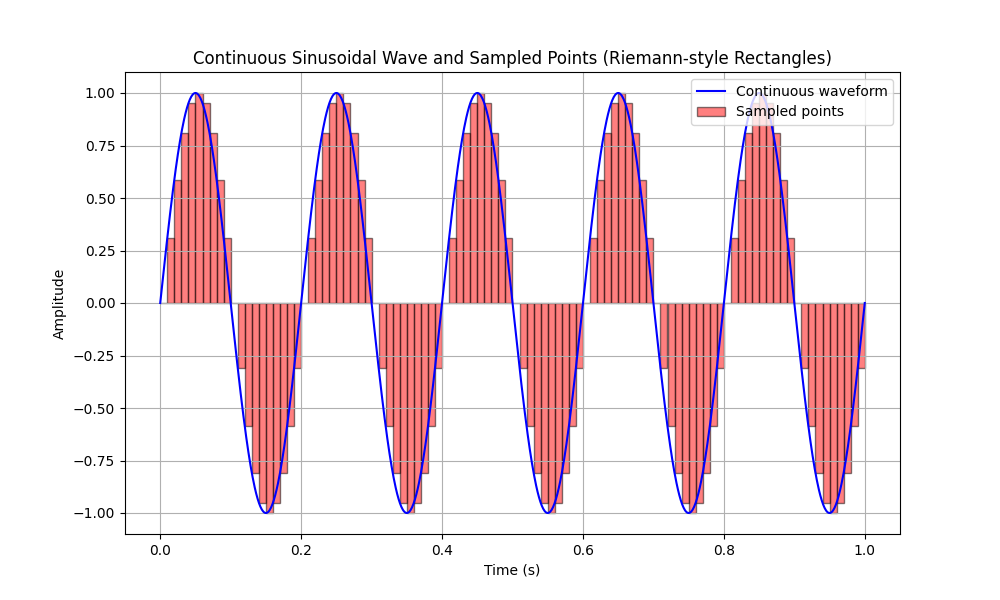
Remember: here the sinusoid is the actual sound - so something that should represent the Vinyl recording, and the boxes represent a (very low sampling) digitalised soundwave.

So, to come back to the wave function we've defined in a previous post, we can rewrite everything as:

$$s(t)= A\cdot\sin(2\pi ft+\phi)$$

let's get rid of $\phi$ just to simplify the notation, so to obtain:

$$\sigma(t_k)=A\cdot\sin(2\pi f kT_c)$$

Defining the normalised frequency as $\varphi=f\cdot F^{-1}$, the latter can be rewritten as 

$$\sigma(t_k)=A\cdot\sin(2\pi \varphi k)$$

It's interesting to note that $\varphi$ represents the number of sinusoidal cycles occurring per sampling period. This essentially tells us how many full oscillations of the wave are captured between samples, which directly impacts the accuracy and fidelity of the digitized sound.

... and this closes the introduction to sampling. In the next post, I'll talk about aliasing.

I promised to tell you a good way to make mr. Knowitall shut the heck up. Here we go. 

If you live in a relatively new house (let's say, built from 1910 onwards, but this depends on the country), chances are that the walls are not made of solid bricks, but of hollow bricks. Now, if you're listening music in a room whose walls are made up of hollowed bricks, you'll introduce a lot of vibrations that are not part of the original sound. Solid bricks don't. This introduces lots of unwanted $phi$'s in your soundwaves, dude! So, the sound is not as pure as it is supposed to be. Further, the stylus of the turntable also consumes the vinylic surface, thus changing the sound. The MoFo will tell you "perhaps, but this is nothing but a small variation..." so you can tell him "and so is the loss of information introduced by the digitalisation process. (you can - actually you should! - end the sentence with "you pointless little dork!"). 

If he keeps spearheading his shit, then run away like hell. Further discussion is like talking about football with a Juventus FC supporter. 

Do you want to stay one step ahead of the Know-it-alls? Subscribe to the newsletter and get the best delivered straight to your inbox (without having to endure a thousand unwanted lectures).