Sound and waveforms

Introduction: this post is rather technical. You shouldn't be a math geek, and yet you oughta be a math geek to grasp all the things here. But don't worry, I've got you covered. There is also a "non-geek" version of this post: you can find it here.

In this post, I want to tackle some basic concepts about sound.

Definition 1: SOUND
Sound is a form of mechanical energy that manifests as pressure variations transmitted through a material medium from one particle to another. These variations result from the kinetic movement of particles, propagating as sound waves. Without a medium, such as in the vacuum of space, sound cannot propagate.

A first consequence of this definition is that molecules move away from their equilibrium position and then return to it; in other words, molecules move back and forth from their equilibrium position. In technical terms, this back-and-forth movement constitutes a complete cycle of compression and rarefaction.

The previous consideration leads to the following:

Definition 2: FREQUENCY
The frequency of a sound represents the number of complete cycles of compression and rarefaction that occur in one second, measured in Hertz (Hz).

Measuring Frequency
Frequency is measured in Hertz (Hz), where 1 Hz corresponds to one cycle per second. For example:

• A sound with a frequency of 500 Hz means that particles undergo 500 cycles of back-and-forth motion every second.
• Higher-frequency sounds (like a high-pitched whistle) have more cycles per second, resulting in higher tones.
• Lower-frequency sounds (like a lion's roar) have fewer cycles per second, resulting in lower tones.

Relevance of Frequency
Frequency is one of the most important aspects in sound perception because it determines the perceived pitch. It is crucial in various contexts:

• Music: Each musical note corresponds to a specific frequency. Instruments are tuned to produce precise frequencies to create harmonious melodies.
• Communications: The ability to transmit and receive at various frequencies is essential in communication technologies, such as radio and telephones.
• Acoustics: Frequency analysis helps design spaces that enhance or control sound propagation, such as theaters, recording studios, and classrooms.

Despite the fact that applications in communications and acoustics are tremendously fascinating, they will not be the focus of the material we will concentrate on for now.

Definition 3: SOUND WAVES
A sound wave can be described as a pattern of disturbance that propagates through a medium, carrying energy from one place to another without transporting matter. Sound waves are a type of mechanical wave and can be mathematically represented as periodic functions.

The periodic functions that describe sound waves are typically sinusoidal due to the oscillating nature of particles moving back and forth from their equilibrium position. These functions are characterized by amplitude, frequency, and phase:

• Amplitude ($A$): Indicates the maximum displacement of the particle from its equilibrium position (the volume of the sound).
• Frequency ($f$): Indicates the number of complete oscillations (cycles) per unit of time (the pitch of the sound).
• Phase ($\phi$): Determines the starting point of the cycle at a given moment.

We have already introduced the concept of frequency. Now, let's talk about the amplitude of a sound wave.
Let’s think about the membrane of a speaker. When it is stimulated, it begins to vibrate. These vibrations displace adjacent air particles (or particles of another medium), creating pressure variations that propagate as sound waves.

As we have already seen, these vibrations are characterised by a frequency, which depends on:

• Vibration Frequency of the Membrane: The speed at which the membrane vibrates determines the fundamental frequency of the sound produced. If the membrane vibrates rapidly, it produces a high-frequency (high-pitched) sound; if it vibrates slowly, the sound will have a low frequency (low-pitched).
• Properties of the Transmission Medium: The characteristics of the medium (such as the density and elasticity of air) influence how the sound wave propagates. These factors do not change the frequency of the wave generated by the membrane, but they affect the propagation speed of the wave and thus the wavelength associated with the frequency.

These vibrations also produce waves characterized by an amplitude.

The amplitude of a sound wave is determined by the amount of energy used to stimulate the membrane:

• Greater Force of Stimulation: If the membrane is struck harder or pushed with more energy, the nearby air particles will be displaced more violently. This produces more intense pressure variations, resulting in a sound wave of greater amplitude, which we perceive as a louder sound.
• Amplitude and Energy: The amplitude of the sound wave is directly proportional to the energy that generates it. Therefore, a wave of greater amplitude carries more energy through the medium.

Let's focus on membranes (the discussion for strings is similar but slightly more complicated due to physical factors that we can analyze separately).

Typically, when a membrane, such as that of a drum or a speaker, is stimulated, it vibrates and generates sound waves that propagate mainly perpendicularly to the membrane's surface. This happens because the membrane pushes and pulls the air particles (or another medium) directly in front of it as it vibrates.

How Propagation Works:

• Vibration of the Membrane: When the membrane vibrates, it moves back and forth from its resting position. During the outward movement, the membrane pushes the air particles, creating a zone of compression. When it moves inward, it leaves behind a zone of rarefaction.
• Direction of the Wave: These pressure changes (compression and rarefaction) are transmitted through the air as longitudinal waves that move perpendicularly to the membrane's surface. This means that the air particles move back and forth in the same direction in which the wave propagates.
• Practical Effect: Sound, therefore, spreads radially from the origin, with the membrane at the center acting as the starting point for waves extending outward.

This arrangement is effective for transferring sound energy from the vibrating object (the membrane) to the surrounding medium efficiently, allowing the sound to travel through the air and reach listeners.

This leads to

Definition 4: WAVE AMPLITUDE
Wave amplitude is the measure of how large the maximum displacement of the medium's particles (e.g., air) is from their equilibrium position when the wave passes through them. Here’s how you can visualize it:

Visualizing Wave Amplitude

• Maximum Displacement: Imagine the membrane of a drum moving forward, pushing the air in front of it. The amplitude of the sound wave is the maximum distance that the air particles move from their resting position due to this push.
• Pressure Wave: When the membrane moves outward, it creates an area of higher pressure (compression) immediately in front of it. The amplitude of this pressure wave is proportional to the force with which the membrane pushes the air; the stronger the push, the greater the amplitude.
• Graphical Visualization: If one could see the sound wave propagating through the air, they would observe peaks and troughs moving radially from the membrane. The peaks represent the areas of maximum compression (where particles are closer together), and the troughs represent areas of rarefaction (where particles are farther apart). The amplitude is the vertical distance from the center of the equilibrium line (the resting position of the particles) to the peak of the compression.
• Relation to Volume: In practical terms, a greater amplitude results in a louder sound because more intense pressure variations stimulate the ear with greater energy.

Finally, we talked about PHASE. The phase $\phi$ represents the initial phase of the wave at time $t=0$. The initial phase is a key concept for describing the wave's position in its cycle at the moment observation begins.

Starting Point of the Wave:
$\phi$ determines the point in the oscillation cycle from which the wave begins. For example, if $\phi=0$, the wave starts at its natural equilibrium point and moves toward the positive maximum. If $\phi=\pi/2$​ (90 degrees), the wave starts at its positive maximum.

Phase Shift Relative to a Reference:
$\phi$ is often used to describe how one wave is shifted relative to another wave of the same type. This is particularly useful in situations where two or more waves interact, such as in interference or the formation of beat patterns.

Practical Applications of $\phi$:

• Interference: In wave interference, the initial phase of each wave determines whether constructive interference (the waves are in phase and add up) or destructive interference (the waves are out of phase and partially or completely cancel each other out) will occur.
• Sound Analysis: In acoustics, different initial phases can be used to create specific sound effects or to analyse how sounds combine in complex environments.
• Signal Technology: In signal transmission, phase modulation can be used to carry information. Changing the phase of a carrier wave according to the data signal is the basis for many forms of digital communication.

Auditory Effects of Phase $\phi$

Sound Interference: When two sound waves with the same frequency but different phases overlap, the relative phase between them can cause constructive interference (when the phases are aligned) or destructive interference (when the phases are opposite). For example:

• Constructive Interference: If $\phi$ is the same for both waves or differs by integer multiples of $2\pi$, their peaks and troughs align, resulting in a louder sound.
• Destructive Interference: If $\phi$ differs by $\pi$ (180 degrees) or odd multiples of $\pi$, the peaks of one wave coincide with the troughs of the other, potentially canceling each other out, resulting in a weaker sound or the disappearance of certain frequencies.

Spatial and Directional Perception of Sound: Changes in the phase between sound waves reaching different ears can influence the perception of the direction from which the sound originates. Our auditory system uses phase differences between the ears to help locate the sound source.

Sound Quality and Timbre: Phase also affects the overall waveform of a sound, which can alter the sound's timbre. Changes in the phase of a sound's harmonic components can modify the perception of its "color" or quality.

Audibly, How Do We "Hear" the Variation of $\phi$ When Playing a Note?

When you play a note on an instrument, changing the phase $\phi$ is usually not something you can directly control, as you would with amplitude or frequency. However, phase can naturally vary due to how the sound wave interacts with the environment (echo, reflection) or with other sound waves from different instruments within an orchestra or a band. These phase changes can subtly affect the richness and fullness of the sound, as well as its spatial and directional interaction.

In practice, a musician modifies phases through tuning and playing technique, which can influence how the phases of different harmonics of a note interact. However, these modifications are often subtle and unconscious, emerging naturally rather than through deliberate adjustments of $\phi$.

One might then ask, "I have a bass. I play a C. If I play it with my fingers, I get a certain $\phi$; if I play it slapping, I get another; if I play it with a pick, I get a third, and so on?"

The idea of varying $\phi$, or initial phase, based on the technique used to play a note on the bass is interesting and has practical grounding, but it’s important to clarify how these differences manifest and influence the sound.

How Does $\phi$ Vary with Playing Technique?

• Differences in $\phi$ Between Techniques: In theory, when playing a C on the bass using different techniques (fingerpicking, slapping, picking), you might indeed influence the initial phase of the produced sound waves. However, these differences are usually very subtle and may not be directly perceived as phase changes, but rather as differences in timbre and the sound's attack.
• Fingerpicking: This technique tends to produce a softer, rounder sound with a less defined attack. The initial phase might be relatively aligned with the natural oscillations of the string.
• Slapping: Produces a sound with a much more pronounced attack and often with more emphasis on higher frequencies. The initial phase might be more variable due to the more energetic impulse and the way the string strikes the fret.
• Picking: Generates a more defined and precise attack compared to fingerpicking, with added brightness from the pick's material. Here, too, the initial impulse might slightly alter the initial phase of the oscillation.

Auditory Effect of Variations in $\phi$: While each technique might technically influence the initial phase, what we perceive auditorily is more of a change in timbre, volume, and sound clarity rather than a clear change in "phase" as an isolated parameter. The differences in timbre between techniques are partly due to the different ways the string is excited, which affect the amplitude and distribution of harmonic frequencies more than the specific initial phase.

$\phi$, or the initial phase of a sound wave, is not determined solely by the playing technique but by a variety of factors that can influence how and when a wave begins its oscillation cycle. Here are some of the factors that can affect the initial phase of a sound:

• Playing Technique: As noted, the way a string is plucked or struck can slightly change the initial phase of the string's oscillation. This includes the use of picks, fingers, or techniques like slapping, each of which can introduce variations in how the string is set into motion.
• Instrument Tuning: The tension of the strings, influenced by the tuning, can alter the characteristics of the string's oscillations, including their starting point relative to the resting position.
• Instrument Materials: The materials used in the instrument's body, bridge, and strings themselves can subtly affect the characteristics of the generated waves, including the initial phase. Different materials have varying elastic and density properties, which influence how vibrations are transferred and propagated.
• Acoustic Environment: The environment in which you play the instrument can affect how sound waves are reflected, absorbed, or transmitted, potentially altering the perceived phase of the sound. For example, a highly reverberant environment can superimpose multiple reflections of the original sound, modifying the perceived phase.
• Interaction with Other Sounds: When playing in an ensemble or with other instruments, the interference between different sound waves can alter the perceived phase of each sound. This can be particularly noticeable in situations with harmonically complex sounds or in acoustically dense spaces.

(Here, I’m talking about the bass, but the same concepts apply to all "non-electronic" instruments.)

A very long discussion that will exhaust the reader's patient can only be worsened by the following observation:

In many practical situations, especially in everyday music and general use of musical instruments, yes, you can generally ignore considerations about the initial phase $\phi$ as an isolated parameter to manage or modify. Here are some reasons why phase $\phi$ might be less critical in these contexts:

• Human Perception: Human perception of sound is generally more sensitive to factors like frequency (which determines pitch), amplitude (which determines volume), and timbre (which is influenced by the overall waveform and the distribution of harmonics) rather than to the specific phase of an isolated sound.
• Complexity of Phase in Realistic Contexts: In musical practice, the phase of a sound can vary significantly due to multiple reflections and interactions in a real listening environment, making it difficult to control or precisely predict the phase of each individual note or sound.
• Phase Interactions Between Sounds: When playing with other instruments or in a complex acoustic environment, phase interactions can become so intricate that attempting to control or predict them individually becomes impractical without advanced instrumentation or detailed acoustic analysis.
• Sound Production and Engineering: In sound engineering and music production, while phase is considered during mixing and mastering—especially in relation to the phase between multiple tracks—the more critical aspects managed in daily practice tend to focus on equalisation, mix levels, and spatial effects.

I feel like I have trolled readers until now 😄 Let's talk math, now!

The magnitudes we have introduced are the foundations to introduce the wave equation

$$ y(t)=A\cdot\sin\left(2\pi f t+\phi\right)$$

where:

• $f$ represents the frequency of the vibration, which determines the pitch of the sound.
• $t$ is the time, showing the wave's progression over time.
• $\phi$ is the initial phase, which determines the starting point of the oscillation cycle in time.
• The function $\sin\left(2\pi f t+\phi\right)$ oscillates between -1 and 1, representing the periodic oscillations of the string around its equilibrium position.
• $A$ is the amplitude of the wave.

Below, some graphs for the function:

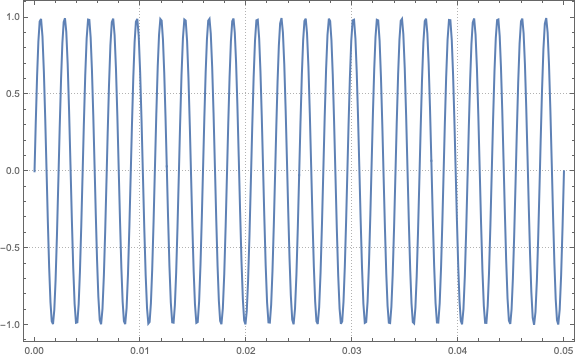
Figure 1: $y(t)=\sin(2\cdot 440\pi t+0)$

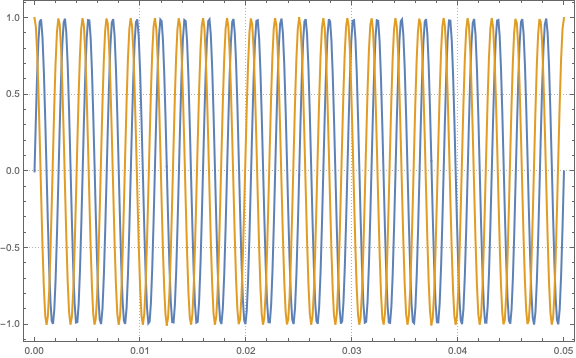
Figure 1: $y(t)=\sin(2\cdot 440\pi t+0)$ in blue, in amber $y(t)=\sin(2\cdot 440\pi t+\pi/2)$

Some observations

Why $2\pi$:

• Complete Cycles: A complete cycle of a sine wave corresponds to a full rotation around a circle. Since the circumference of a circle is $2\pi$ radians, a complete cycle of a sine wave, from a mathematical perspective, covers $2\pi$ radians. Therefore, to transform an oscillation from a temporal context to a circular spatial context, we use $2\pi$.
• Frequency and Period: The frequency $f$ of a wave indicates how many times the wave completes a cycle in one second. The period $T$ of a wave is the time it takes to complete one cycle, and $T=1/f$​. To obtain the number of complete cycles in a given time $t$, we multiply $f$ by $t$. However, to convert this number into radians (the unit used in trigonometric functions like sine and cosine), we need to multiply it by $2\pi$.

The Formula $2\pi ft$

In the equation of a sound wave $y(t)=A\sin⁡(2\pi ft+\phi)$

• $2\pi ft$ calculates the angle in radians for a given time tt:
  • $f$ is the frequency of the wave in Hz (cycles per second).
  • $t$ is the time in seconds.
• $2\pi f$ is the angular velocity of the wave, which means how many radians per second the wave travels.
• By multiplying by $t$, we obtain the total angle in radians that the wave has traveled up to the time $t$.

Observation: If I pluck the string of a bass, the note will gradually "fade out" – what happens physically? Does $A$ decrease over time?

When you pluck the string of a bass and notice that the sound gradually fades out, this phenomenon is due to the decrease in the amplitude of the vibrations over time. Physically, several factors contribute to this "fading out" or decay of sound.

Factors Causing Sound Decay:

• Energy Dissipation: The vibrations of the string transfer energy to the surrounding air and other parts of the instrument, such as the bridge, body, and neck. This energy transfer manifests as sound waves in the air. As the energy is transferred, the amount of energy left in the string decreases, thereby reducing the amplitude of its vibrations.
• Internal and Air Friction: The internal friction within the string and the friction with the air (viscous dissipation) further dampen the vibrations. The air resistance and internal friction of the materials of the string and the instrument convert some of the mechanical energy into heat, decreasing the energy available to sustain the vibratory motion.
• Acoustic Absorption: Part of the sound energy is absorbed by the body of the instrument and, if in an enclosed environment, also by the surrounding surfaces like walls, ceilings, and floors. This absorption further reduces the intensity of the perceived sound.

Mathematical Modelling of Decay

In mathematical terms, the decay can be modelled by modifying the wave equation to include a term that represents the decrease in amplitude over time. The time-varying amplitude can be expressed as:

$$y(t)=A(t)\sin⁡(2\pi ft+\phi)

where $A(t)$ is the function that describes how the amplitude decreases over time. This is often modeled as a decreasing exponential function:

$$A(t)=A_0\exp(-\alpha t)$$

• $A_0$​ is the initial amplitude at time $t=0$.
• $\alpha$ is the decay constant that describes how quickly the sound fades; a larger value of αα indicates a faster decay.

Origin and Influence of $\alpha$

The constant $\alpha$ represents the rate of sound decay and is influenced by several factors:

• Physical Properties of the Instrument: The construction, materials, and tension of the strings affect the value of $\alpha$. Different instruments will have different decay rates depending on how well they sustain vibrations.
• Interaction with the Environment: The environment in which the sound is produced can influence its dissipation. A highly absorbent or open space can cause a faster decay compared to a more resonant room.
• Aerodynamic and Mechanical Effects: Air resistance and the transfer of energy within the instrument contribute to the decay.
• Design Parameters: In some instruments, αα can be intentionally modified through design or built-in electronics to shape the sound.

Determination and Use of $\alpha$

In practice, $\alpha$ is often determined empirically through measurements and experimentation. In the physics and engineering of sound, it can be calculated by analysing how the sound energy decreases over time. In sound design and music production, the value of $\alpha$ can be artificially adjusted using effects to create the desired sound character.

In conclusion, sound decay is a natural process mathematically represented by the decrease in amplitude over time, modelled by the constant $\alpha$. This phenomenon is influenced by a combination of physical, environmental, and technological factors.

The graph of a decay can be represented as the image below:

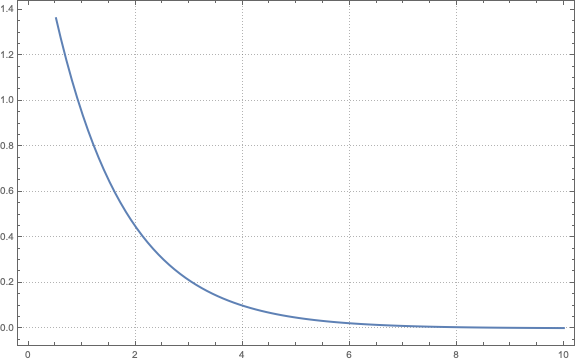
Figure 3: $A(t)=2\exp(-.75\cdot t)$

Putting all together, we obtain a waveform as the following:

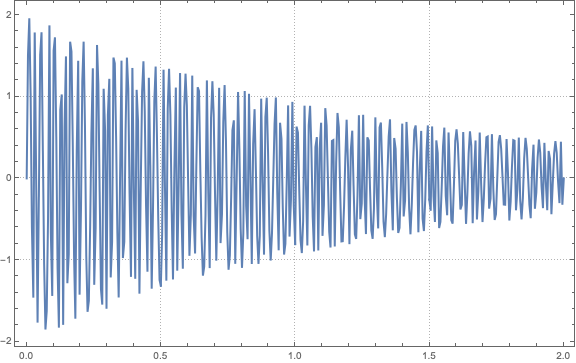
Figure 4: Applying the decay model at the first soundwave.

In the next article, I will talk about the timber of a sound.